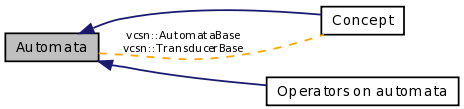
Automata
Collaboration diagram for Automata:
Automaton constructs for Vaucanson.
More...
Detailed Description
Automaton constructs for Vaucanson.
- See also:
- vcsn::automata
- vcsn::automata::AlphabetSet
- vcsn::automata::MonoidBase
- vcsn::automata::FreeMonoid
- vcsn::automata::FreeMonoidProduct
Theoretical context
The striking feature of automata is the versatility of the concept - a labeled oriented graph - and its ability to models so many different kinds of machines simply by varying the domains where the labels are taken.
This chapter presents the kinds of automata Vaucanson has been designed to work on. First, naive definitions are given to remind the reader what is a Boolean automaton from a theoretical point of view. Then, more elaborated definitions are given to provide a generalized context in which it is possible to define weighted automata. Finally, this chapter explains how this formalism is used to represent transducers. The interested reader may find far more advanced descriptions and definitions in 03sakarovitch.
This section gives some well known definitions about Boolean automata. Those should be rather usual to the experienced reader. A first definition introduces basic letter automata while a second one presents Boolean automata with spontaneous transitions.
Definition 1 A Boolean letter automaton is a 5-tuple
with:
-
an alphabet,
-
a finite set of state,
-
a set of transitions,
-
a set of initial states, and
-
a set of final states.
Figure 1.1: A simple Boolean automaton recognizing the language of words which contain a b.
| |
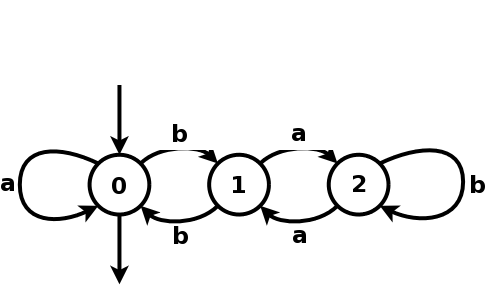
Figure 1.2: A Boolean automaton recognizing the language of binary numbers that are divisible by 3 (with a as 0 and b as 1).
| |
Figures 1.1 and 1.2 show some examples of Boolean automata. A word
of length
is said to be recognized by an automaton
if there exist a path from an initial state to a final state labeled with the word, i.e. a sequence of
consecutive transitions
Spontaneous transitions
It is common to add to the previous definition the ability for an automaton to have ``spontaneous transitions''. Such transitions are not labeled by any letter and can be ``triggered'' at any time during the evaluation of an automaton. This give definition 2.
Definition 2 A Boolean automaton with spontaneous transitions is a 6-tuple
with:
-
an alphabet,
-
a finite set of states,
-
a set of transitions,
-
a set of spontaneous transitions,
-
a set of initial states, and
-
a set of final states.
|
The evaluation of such an automaton is performed as for other letter automata, but spontaneous transitions may be part of the path.
Boolean automata are devices designed to recognize and represent a particular class of languages. This section introduces another class of automata that are able to perform some computations on words instead of just recognizing them. This class is the class of weighted automata. First, the concept is presented and then a more complete formalism will be given.
Basis
Basically, the transitions of weighted automata are labeled with a weight and a letter. Initial and final states are also labeled with a weight. For a given path from an initial to a final state, it is possible to compute a value. Each weight of the path is multiplied, including the weights from the initial and the final state. An example is given in figure 1.3.
Figure 1.3: Evaluation with a deterministic weighted automaton.
[-1cm]
|
When a weighted automaton is deterministic, its evaluation for a given word is straightforward. Either there exists a unique path labeled with the evaluated word from an initial state to a final one, and the result is computed as explained above, either there exist no such path and the result evaluates to zero.
However, with non-deterministic weighted
automata, there may exist several paths from an initial to a final state that are labeled with the same word. In that case, such a word evaluates to the sum of the evaluation of each path. An example is given in figure
1.4.
Figure 1.4: Evaluation with a non-deterministic weighted automaton.
This weighted automaton computes the value of a number from its binary representation. Thus, if a is considered to be 0 and b to be 1, the word babb (1011) evaluates to 11. |
|
Furthermore, it is not mandatory for a weighted automaton to use the usual addition and multiplication. In fact the weight may be in any set, provided it is equipped with two
internal laws that provide the structure of a semiring, as defined in
3.
Definition 3
is a semiring, if and only if:
-
is a commutative monoid which neutral element is noted
,
-
is a monoid which neutral element is noted
,
-
is distributive on
, and
-
.
A weighted automaton is always defined over a particular semiring. It is worth noting that ``Classical'' Boolean
automata are just weighted
automata over
that maps a letter
to
true if a transition exists on
.
Definition 4 A
weighted letter automaton is a 6-tuple
with:
-
an alphabet,
-
a semiring,
-
a finite set of states,
-
a set of transitions,
-
a set of initial states, and
-
a set of final states.
Definition
4 does not provide any support for spontaneous transitions. However, transitions on
automata are not necessarily letter or spontaneous transitions. They may be polynomials (
e.g.
) or even rational expressions (
e.g.
). In a more general way transitions are defined to be
series, as given in definition
5.
Definition 5 A series from a monoid
to a semiring
, noted as an element of the set
, is an application which maps elements of
to elements of
.
The smallest set that contains all polynoms on
with coefficients into
and which is closed using the star operation is the set of
-rational series on
, noted
.
At a basic level, rational series may be used to define rational languages. Thus a Boolean series in
which maps words from a free monoid
over an alphabet
to Boolean values
true or
false may be viewed as an indicator function for a language.
is exactly the set of rational expressions on the alphabet
.
Equipped with those definitions, it is now possible to formally define an automaton.
Definition 6 A
-automaton is a 6-tuple
with:
-
a monoid,
-
a semiring,
-
a finite set of states,
-
a set of transitions,
-
a set of initial states, and
-
a set of final states.
Using definition
6, a letter transition for a Boolean automaton is a transition labeled by a series that maps a specific letter to true and everything else to false. A spontaneous transition is a transition which support is the empty word and a weighted letter transition is a transition which support has one unique letter.
In the particular case where
(with
an alphabet),
and each transition's label is just a letter, we fall back in the ``usual case'' of ``traditional'' Boolean
automata.
Of course this definition covers a wide variety of
automata. In particular, note that the ``input'' of the automaton is not necessarily a free monoid. Therefore, it is not required for inputs to be decomposable in letters in a unique fashion. Also, there is no special restriction on an automaton transition's labels. Typically these labels are just letters, but nothing prohibits them to be words or even rational expressions. Such an automaton is shown in figure
1.5.
Figure 1.5: The automaton of figure 1.4, with rational expressions as labels.
| |
The evaluation of such an automaton for a given input is not possible in general. When
is a free monoid, each member of it (so called words) is decomposable into a unique sequence of letters, and the evaluation may be defined in the case transitions are also labeled with letters.
As will be seen in the next section, definition
6 is general enough to include transducers, provided good monoids and semirings are used. To ensure a maximal genericity and mathematical consistency, V
AUCANSON uses this definition to work on any kind of Boolean
automata, weighted
automata or transducers.
Transducers are a special kind of
automata that are designed to ``translate'' rational languages into other rational languages. While the evaluation of a weighted automaton gives weights, the evaluation of a transducer gives another word. The input alphabet and the output alphabet are not necessarily equal. An example of transducer is given in figure
1.6.
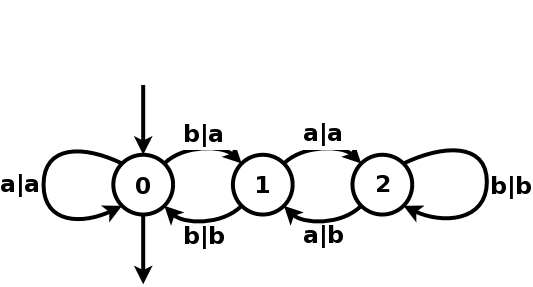
Figure 1.6: A transducer that divides binary numbers by 3.
|
On the graphical representation of a transducer, the letters on the left hand side of | represent the input letters and the letters on the right hand side represent output letters.
This transducer works on the alphabet
. It expects a binary number as input, a being the digit 0 and b being the digit 1. The output consists in the binary representation of the input divided by 3. As an example, bba (110 or 6) gives abb (010 or 2). |
|
Using the formalism of definition
6 it is possible to define transducers in two different ways:
-
following a classical approach, a transducer from an alphabet
to an alphabet
may be viewed as a Boolean automaton over the monoid
.
-
with the union and concatenation operators from the rational languages forms a semiring. Therefore a weighted automaton over
which weights are in
also represents a transducer.
Of course, a transducer may have arbitrarily complex labels, as shown in figure
1.7. In this example, some initial or final states do produce output and some transitions may produce several letters as output.
Figure 1.7: A complex transducer which replaces every occurrence of abb with yxx.
| |
Transducers are currently being implemented in V
AUCANSON. Although it is possible to build transducers and run various algorithms on them, their support is less complete than for other
automata. 04oconnor provides information about the implementation of transducers in V
AUCANSON.
- vcsn::automata::SemigroupBase
- vcsn::automata::NumericalSemiring
- vcsn::automata::TropicalSemiring
- vcsn::automata::Series
Generated on Sun Jul 29 19:47:34 2007 for Vaucanson by
 1.5.2
1.5.2

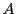
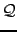
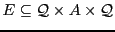
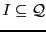
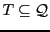
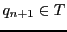
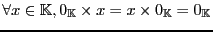
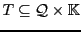
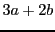
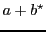
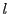
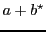
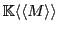
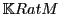
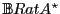
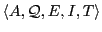
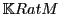
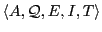
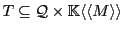
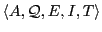
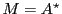
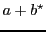
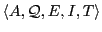
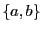
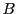
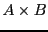
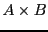
 1.5.2
1.5.2